Get Land

Owner:

Greg

Solution:

UNWIND

GC Notes:

GC to update day-of-game.

Presentation:

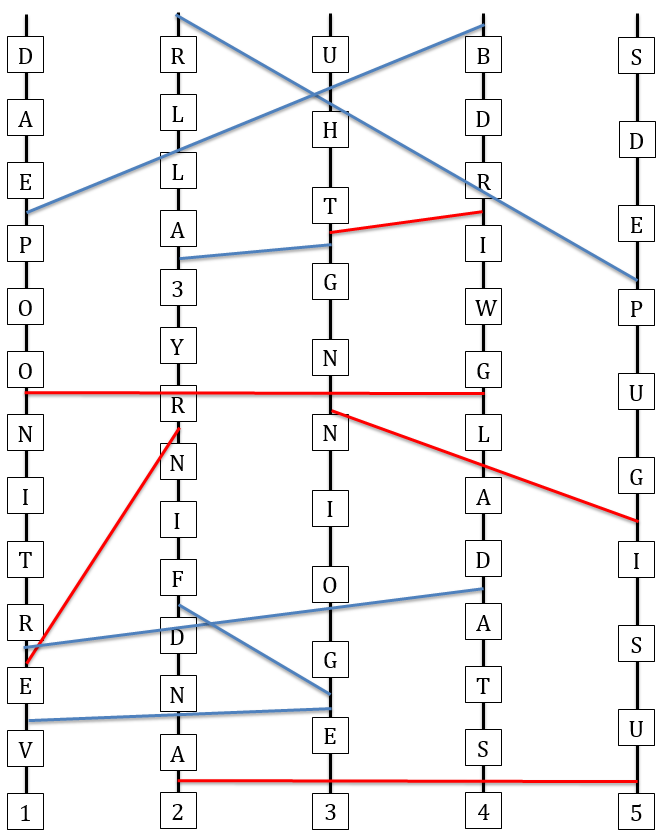
The teams see Rapunzel's "hair": a set of tangled-up ropes hanging from a staircase or something. The ropes have "beads" with numbers or letters on them, and blue or red "ribbons" connecting them at various points.

They also receive a data collection sheet. The graphs in the Guide are formatted similarly to the data collection sheet, but with the strands reordered in a way that makes the connections clearer. A filled-in version of that sheet is at the bottom of the page.

Walkthrough:

Part of the difficulty is just collecting the data. Obviously the order of letters is important, and wherever there's a ribbon the point it connects on both strands is important. (And when there are two ribbons that connect between the same pair of buoys/beads, which one is on top is important.)

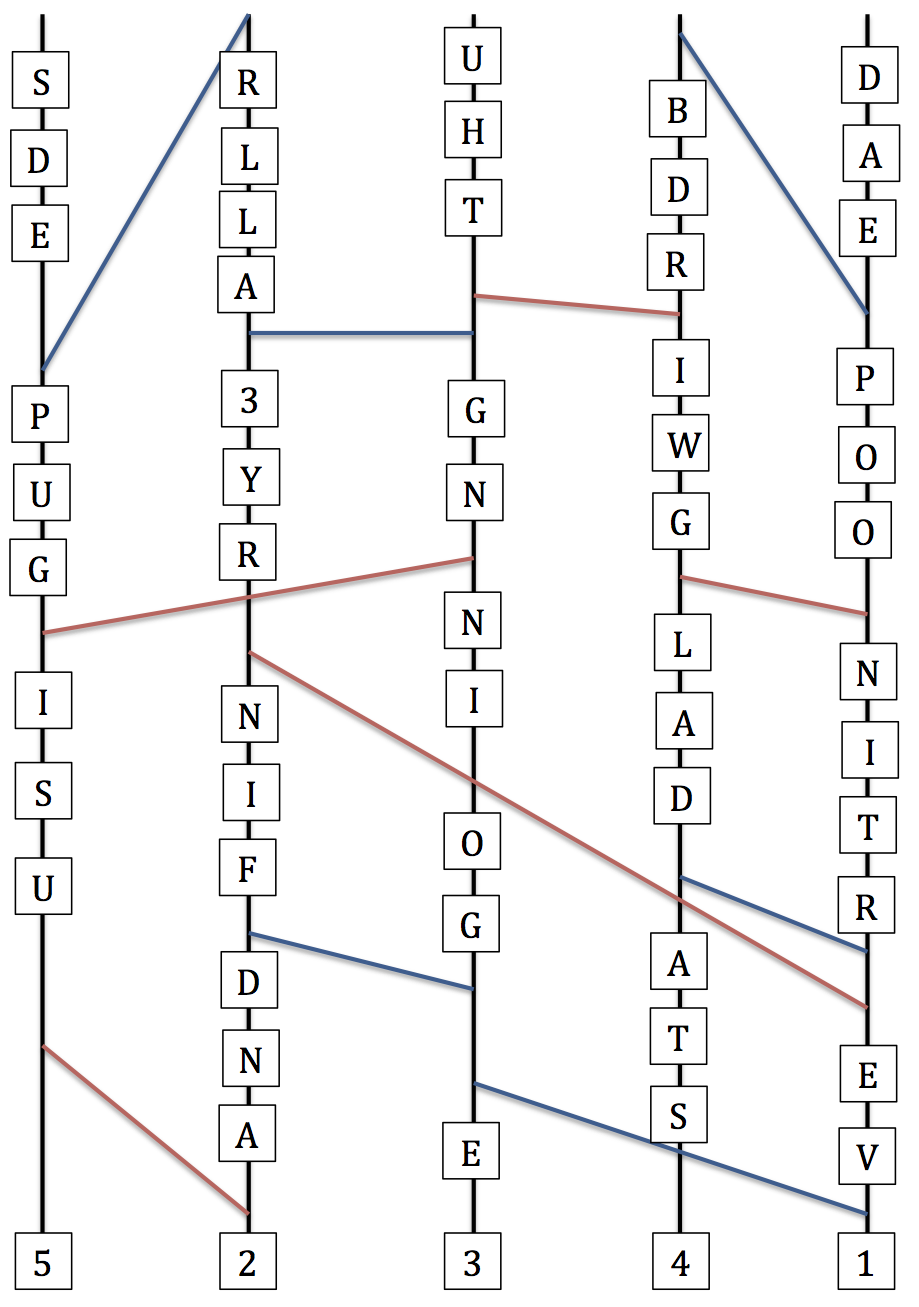
Reading the strands directly is garbage. The way to get useful data is to use the ribbons as connectors between the strands: start at the bottom of one strand, and whenever you reach a ribbon cross over to its other side. That yields five phrases that can be put together (ordered by the number at the bottom of the strand) into a set of instructions:

1: FIND A LOOP

2: USING ALL REDS

3: EVERY 3RD BEAD

4: STARTING WITH U

5: AND GOING UP

The five red ribbons can be used to form a loop that crosses over all the strands (sometimes going up and sometimes down):

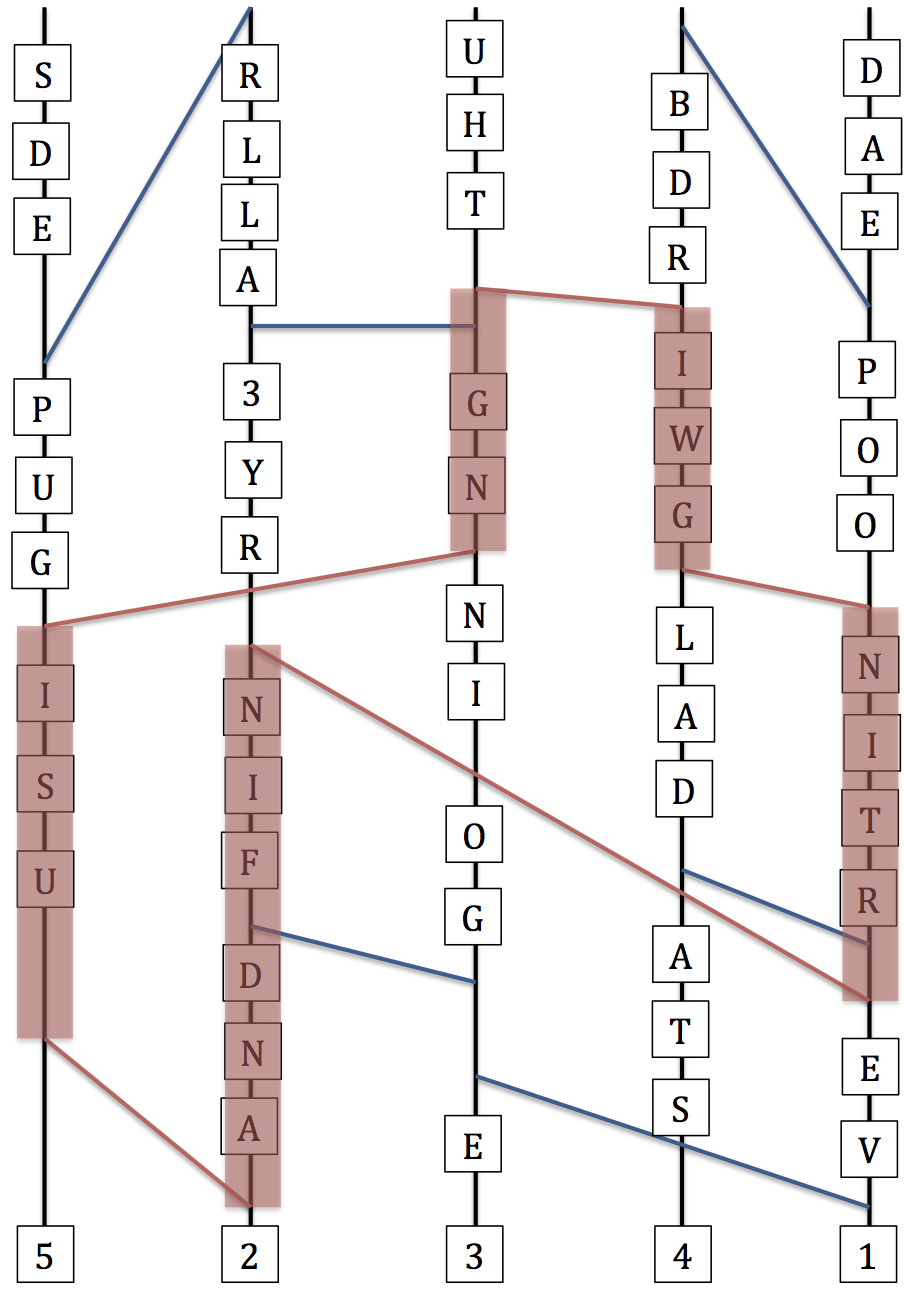
Starting at the only U on the loop, and going up on that strand, the letters on the loop are USINGIWGNITRNIFDNA. Reading every third bead yields the answer, UNWIND.

Hinting:

Be fairly generous about confirming data. The two copies of the puzzle are identical, so teams can divide and conquer, or a spot that's ambiguous on one might be less ambiguous on the other.

Some teams want the final loop to always go up, and sometimes try to use blue ribbons to make that happen. ("It says ALL REDS, not ONLY REDS") That's provably impossible*, so nudge them that maybe one of their other assumptions is invalid.

*Look at the red ribbon between strands 3 and 4. If the loop always goes up, it must go up from one of the ends of that ribbon. If it goes up from strand 3, it gets to the top of the rope immediately. If it goes up from strand 4, it either hits the top or takes a blue ribbon to strand 1 and hits the top. QED.

Data:

The filled-out version of the sheet as the teams got it: