Digging
Owner:
Bennett (Skyler Goodell for the event)
Solution:
UNDIGNIFIED
GC Notes:
GC to update day-of-game.
Presentation:
The interns arrive on a beach and meet a confused pirate. He points them towards an instance of the puzzle on the beach. That puzzle has 5 wooden stakes that are connected with twine to create 4 connected segments. At the beginning of the first segment there is a shovel thrust into the sand head first. The shovel has a number of markings along its shaft. It also has a piece of paper rubber-banded around the shaft. The piece of paper is a letter and tells them that a pirate buried some treasure on the beach but has been hit on the head a few times and can’t remember where the puzzle. The letter says that there is a message on the shovel explaining how to find the path. The first few segments of the path have been given to them both on a sheet of graph paper along with the letter and marked out for them at scale using twine and stakes in the sand. The pirate who buried the treasure is present and while his memory is "fuzzy" there are rules that allow the interns to check with the pirate periodically and confirm that they are on the right track. Their goal is to figure out the rest of the path from the shovel and dig up the buried treasure at the end of it.
Walkthrough:
In brief
Translate the lines and diamonds on the shovel into semaphore. Imagine a diamond and the two lines that share its vertical position as points around the edge of a circle. Rotate the shovel to orient the diamond as the top of that circle. The lines then indicate where the flags would be for semaphore. Read from the top of the shovel down to the head of the shovel.
- Intermediate answer: OVERLAPSHAREDFLAGARMS
Construct the path by overlapping each semaphore with the previous semaphore. You decide which arms of the semaphores to overlap by looking at which arms share a single line on the shovel.
Pirate on site simplifies the path and the interns dig up the answer at the end of it. Answer will be UNDIGNIFIED.
Reading the Semaphores
The shaft of the shovel (oriented with the head of the shovel down), can be interpreted as a series of semaphores, which spell out a message telling you how to connect those same semaphores together to form a path. With the first part of the path already drawn for the interns in the sand of the beach, they can use what they’ve figured out to complete it and find the treasure.
The encoding on the shovel consists of a series of lines and diamonds. Diamonds are all intended to be the same size and shape. Lines are also all the same length, except for the half-length lines at the top and bottom of the shovel. Each line is drawn vertically on the shovel, positioned around the cylinder at one of the eight cardinal directions. Diamonds are also positioned at one of the eight cardinal directions. Lines are colored either red or blue. With the exception of the half-length lines at the top and the bottom of the shovel, the first half of every line overlaps vertically the previous line and the second half of every shovel overlaps vertically the next line. Red lines only overlap with blue lines and vice versa. This means that at any point on the shovel, there are exactly two overlapping lines, one red and one blue. There is one black diamond for each section of overlapping lines.
Every diamond has a red and a blue line that each share its vertical position (as can be seen in the picture at the end of this section). Imagine that you took a horizontal cross section of the shovel right through the middle of the diamond. You would get a circle with three points of interest around the edges. One point would be where the diamond is around the outside of the circle, the other two where the lines are. If you orient the circle such that the diamond is the top of that circle, the other two points can be read as a semaphore letter.
Let’s take another look at the picture, specifically the part highlighted in the red box. Imagine rotating the shovel such that the diamond in the picture is the top of a circle. That puts the line immediately to the right of it in the picture on the northwest edge of that circle and the other line on the west edge of the circle. That makes the part of the encoding inside the red box translate to an O in semaphore.

On the left: An overlapping section of two lines and the corresponding diamond. For RTM, one of those lines is red and the other is blue.
On the right: Semaphore for the letter O, with a diamond and two circles that correspond with the diamond and two lines in the previous figure and in the accompanying paragraph.
If you read all the semaphores from top to bottom, you get OVERLAPSHAREDFLAGARMS.
Constructing the Path
OVERLAPSHAREDFLAGARMS indicates that, for each semaphore, you overlap one of its two arms with one of the two arms from the previous semaphore. This chains all the semaphores of the message together, building a path. But how do you know which of the first semaphore overlaps with which arm of the next? Go back to the shovel. Each full-length line is used in two semaphores. The first half of any line indicates one of the flag arms of one semaphore and the second half of that line indicates one of the flag arms of the next semaphore. You overlap semaphore arms that share the same line, rotating the second of the two semaphores if necessary.
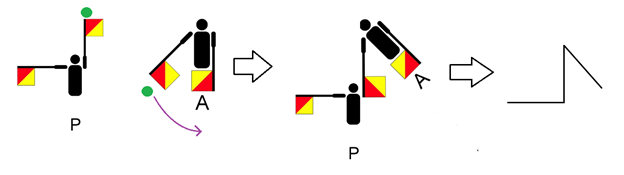
Picture: An example of overlapping a P followed by an A, where the arms marked by the green dots are denoted using the same line on the shovel.
While OVERLAPSHAREDFLAGARMS will always have the same series of semaphores, by changing which arm of a semaphore overlaps with the arm of the previous semaphore you can create a variety of different paths from this one phrase. This allows multiple teams to solve puzzle next to each other without cheating off each other, provided that they are given shovels that create different paths out of OVERLAPSHAREDFLAGARMS
Following the Path
The first four segments of the path are marked out in stakes and twine at full scale for the interns in the sand on the beach (and on their paper on a smaller scale). Each segment of the path is the length of the shovel. Once they have figured out the rest of the path and bring that solution to the pirate, the pirate will simplify the path for them. He does this by canceling out movements that go in opposite directions, and then rearranging the segments so that all the segments going in one direction happen consecutively (e.g. NSEWEW would become EEWW). The interns then follow the simplified path, starting from where the original path was drawn in the sand using the shovel to measure the length of each segment.
Hinting:
Ratholing
In general, when solvers on this puzzle rathole, they do it in one of two ways.
Trying to capture the information from the shovel on paper and work out the puzzle entirely from there.
The encoding on this shovel heavily relies upon being drawn on a cylinder. It’s generally hard to capture all of the relationships necessary on paper in a format that can replace needing to look at the shovel. For example, the fact that the lines can be thought of as points around the edge of a circle (and thus translate to semaphore) is hard to see on paper but not as hard to see when looking at the shovel itself.
This isn’t to say that transferring data to paper is never useful. But it’s better when only used as an aid instead of as a replacement for the shovel. Teams will have a lot harder of a time if they try to ignore the shovel once they feel that they’ve captured all of its data on paper.
- Trying to directly translate the marks on the shovel into a path rather than trying to decode a message from them that explains how to build a path, as the letter tells them to do.
FAQ from Solvers
Each of these is an example of a type of question asked by different playtesters if they called GC and GC responses that helped. The GC responses listed under each question get progressively more specific, a lot of the time teams only needed the first question or so before they understood what to do next.
"GC, we’ve tried a bunch of ways of turning these lines and diamonds into a path but nothing seems to work."
It sounds like you may have skipped an intermediate step.
Was there anything on the letter about what was actually written on the shovel?
Did the letter mention a message? As in an explanation? Or series of directions?
Maybe you should try looking for a message before you try and construct the path?
"GC, we’ve tried a bunch of ways of translating this shovel into morse code, but nothing seems to work."
Maybe you should try something besides morse code.
Have you noticed anything about how the lines and diamonds are grouped?
- See if they mention anything about grouped in 8 rows or columns along the shaft of the shovel.
- What encodings do you know use points along the edge of a circle?
"GC, we’ve got OVERLAPSHAREDFLAGARMS. What do we do? There aren’t any flags around here or anything."
How did you get that?
- Prompting them for semaphore.
Can that involve flags in some way?
Or arms holding flags?
"GC, we get that we’re supposed to overlap one arm of a semaphore with the next, but we can’t figure out which arms of two semaphores overlap?"
Is there somewhere you can get more data that might help with this?
How about going back to the shovel, is there any other data on there?
Is there anything on the shovel that connects semaphores to each other?
